Numero di Nepero: una costante universale

Il numero di Nepero o “e”: cos’è e cosa significa?

Immaginiamo di avere in banca 1$; la stessa banca ci propone un tasso d’interesse del 100% ogni anno. Alla fine dell’anno avremo 1$+100%·1$=2$. Valutiamo invece la seguente proposta: un tasso del 50% (1/2) ma 2 volte l’anno. Conviene? Si, ed ecco la dimostrazione. Dopo i primi 6 mesi avremo 1$+50%·1$=1$+0.5$=1.5$ mentre dopo il secondo mese (alla fine dell’anno) avremo 1.5$+50%·1.5$=1.5$+0.75$=2.25$. Se invece avessimo un tasso di 1/12 (8.3%)  ma 12 volte l’anno (una volta al mese) si può calcolare che arriveremmo alla fine dell’anno con 2.613$. La relazione che lega i soldi alla fine dell’anno (y) con n è:

\(\)\[ y=\left(1+\frac{1}{n}\right)^n \]\(\)

Come si vede, al crescere di n (chiamiamo così il numero di volte l’anno in cui viene applicato il tasso) aumentano anche i soldi. Ecco un grafico del bottino a fine anno (asse y) a crescere di n (asse x).

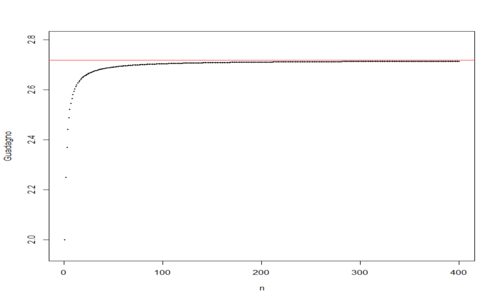
Come si può facilmente dedurre, al crescere di n il valore dei soldi ha una maggiore densità e tende ad un valore compreso tra 2.6 e 2.8, rappresentato dalla linea rossa orizzontale. Il numero di Nepero (o più brevemente “e”) vale infatti 2.718282 ed è rappresentato matematicamente da

\(\)\[ e=\lim_{n\to +\infty}{\left(1+\frac{1}{n}\right)^n} \]\(\)

ed è chiara la relazione con la quantità trovata precedentemente. Con “lim” che sta per “limite” si intende far crescere sempre di più n. Esistono anche altre definizioni che sono però matematicamente complesse. In economia rientra nel campo dell’interesse composto continuo.

Il numero di Nepero, storia e curiosità

La storia di e è legata a quella dei logaritmi (il logaritmo non è altro che l’inverso dell’esponenziale, di cui parleremo più avanti) e al matematico John Napier (italianizzato Nepero), che lavorò proprio con esponenziali e logaritmi. La primissima espressione di e come costante venne trovata dal matematico svizzero Jacob Bernoulli, il quale, intento a calcolare il limite che abbiamo incontrato prima, stabilì che il risultato era compreso proprio tra 2 e 3. La prima traccia del risultato e=2,71828…  si trova in due lettere del celeberrimo matematico Leibniz. La lettera “e” che oggi usiamo compare nel 1727 nel volume Mechanica del matematico svizzero Eulero. È ignota e misteriosa la motivazione della lettera: potrebbe stare per “esponenziale” oppure è un autoriferimento all’autore o più semplicemente… le altre lettere erano già occupate! È inoltre proprio di Eulero una primitiva ma affascinante applicazione della nuova costante in ambito economico, molto simile all’esempio sopracitato.

Una costante “magica”: alcune interessanti proprietà

Il numero di Nepero è un numero irrazionale come pi greco, cioè non termina mai e non presenta alcuna sequenza periodica. È inoltre fondamentale in matematica nei logaritmi ed esponenziali: la funzione esponenziale

\(\)\[ y=e^x \]\(\)

è una delle più importanti in algebra. Osserviamo il suo grafico sul piano cartesiano (la linea blu).

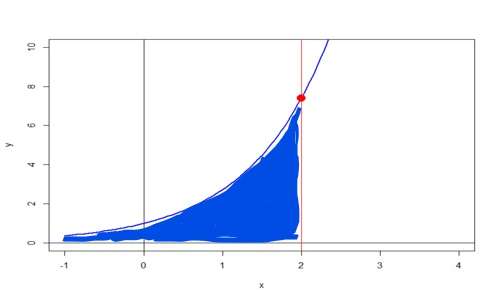
La derivata di una funzione in un punto è un concetto matematico che indica la pendenza della curva in quel punto. La derivata dell’esponenziale “naturale” (chiamiamo così questa funzione) è l’esponenziale stesso, cioè in ogni punto x la pendenza della funzione è e^x. Il risultato è intuitivo anche solo guardando il grafico: all’inizio i valori di y crescono lentamente (quando y è compresa tra 0 e 2), successivamente si ingrandiscono velocemente. Allo stesso modo la pendenza della curva blu (provate ad immaginarla come una montagna da scalare) è inizialmente moderata mentre è più importante man mano che y cresce. Immaginiamo inoltre di “tagliare” la funzione ad x=2 (linea rossa) e di voler calcolare l’area compresa tra l’asse x e la curva (area blu). In analisi matematica questa operazione prende il nome di integrale definito: ebbene, l’area è semplicemente e^x, quindi nel nostro caso l’area blu vale e^2=7.389056. L’esponenziale “naturale” è l’unica funzione matematica a godere di queste fantastiche proprietà.

Un piccolo numero in mille formule

Oltre ad esistere numerose funzioni con il numero di Nepero, come già detto si può trovare un numerose formule: eccone alcune.

\(\)\[ e^{i\pi}+1=0 \]\(\)

Si chiama identità di Eulero ed è considerate tra le formule più belle ed eleganti: essa racchiude infatti il numero 0, l’identità reale 1, l’identità immaginaria “i” e le 2 costanti più importanti: “e” e pi greco.

\(\)\[ f(x)=\frac{1}{\sigma\sqrt{2\pi}} · e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2} \]\(\)

È la formula della distribuzione gaussiana o normale: forma la cosiddetta “campana” di Gauss ed è la più importante in ambito statistico-probabilistico. Qualunque misurazione segue questo andamento, dall’altezza degli individui agli errori di misura nella posizione di una stella.

\(\)\[ f(x)=e^{-\lambda x} \]\(\)

Appartiene alla stessa famiglia della gaussiana, ovvero quelle che si chiamano “variabili aleatorie o casuali”. Si chiama proprio esponenziale e si usa per misurare la “durata di vita” di un fenomeno, come la durata di un apparecchio elettronico o la vita di una particella radioattiva prima di decadere.

\(\)\[ N=N_0· e^{-\frac{t}{\tau}} \]\(\)

In fisica nucleare è una formula che indica il decadimento radioattivo: infatti se al tempo t0=0 sono presenti N0 atomi instabili al tempo t ne rimarranno N (τ è una costante). Si veda l’interessante analogia con la precedente dicitura.