Disequazioni lineari: una overview dei vari tipi

DISEQUAZIONI LINEARI: PERCHÉ ESISTONO

Le disequazioni lineari sono disuguaglianze tra due espressioni, di cui almeno una contiene un’incognita. Le disuguaglianze, in matematica come nel mondo, sono disparità di valori. Ad esempio l’Istana Nurul Iman, il Palazzo in cui dimora il Sultano dello Stato del Brunei (nel Sud-Est asiatico), conta 1788 camere escludendo i bagni, un numero decisamente più grande rispetto ad un semplice appartamento in cui non ce ne sono più di 3, in media. In questo caso, la disuguaglianza è:

\(\)\[1788>3.\]\(\)

Facciamo un passo avanti verso il concetto di disequazioni. Supponiamo che una persona si sia messa alla guida di un veicolo dopo aver assunto alcol e, di ritorno a casa, venga fermato dalla polizia che le effettua un alcol test. Attualmente, la soglia limite di alcol nel sangue consentita dalla legge per una guida sicura è di 0.5 g/L, superata la quale scatta la multa. Se chiamiamo x la quantità di alcol nel sangue, dunque, deve valere:

\(\)\[x \leq 0.5 \, g/L. \]\(\)

Questa è una disequazione, introdotta per indicare che il massimo valore che x può assumere è 0.5, compreso 0.5 stesso in quanto il simbolo è “\(\leq\)”, “minore o uguale”. (Se ti interessa come viene misurata la quantità di alcol nel sangue, leggi l’articolo Come funziona l’alcol test). Per esteso, queste disequazioni vengono definite per esteso disequazioni lineari, o di primo grado, in quanto presentano l’incognita x alla potenza 1. Invece, quelle che hanno almeno un termine incognito con potenza dal 2 in poi, si chiamano disequazioni non lineari (per esempio di secondo grado), che qui non tratteremo.

Equivalenza nelle disequazioni

Le disequazioni lineari di primo grado si basano su due principi di equivalenza. Come, si parla di equivalenza nelle disequazioni? Potrà sembrare una contraddizione, ma in realtà non lo è: l’equivalenza, infatti, non è tra i due membri (i due lati) della disequazione, ma proprio tra due disequazioni. Facciamo un esempio per comprendere meglio il concetto. Consideriamo inizialmente questa disequazione:

\(\)\[x>2.\]\(\)

Se ad entrambe le estremità (che si chiamano membri della disequazione) sommiamo lo stesso numero, ad esempio +3, otteniamo:

\(\)\[x+3>2+3 \rightarrow x+3>5.\]\(\)

La disequazione risulta ancora valida perché se già prima x era maggiore di 2, lo sarà anche adesso che abbiamo aggiunto la stessa quantità ad entrambi. Si dice che \(x+3>5\) è equivalente a \(x>2\). Per visualizzarlo, basti pensare a due ragazzi, uno alto 1.72 m, l’altro 1.76 m. Il secondo è più alto del primo. Se entrambi indossano lo stesso tipo di scarpe con la stessa suola di 3 cm, le altezze totali diventeranno rispettivamente 1.75 m e 1.79 m: è evidente che il secondo ragazzo risulta sempre più alto del primo. Questo si chiama primo principio di equivalenza o monotonia dell’addizione (quest’ultimo nome è di solito usato dai matematici più snob), e in realtà vale anche se si sottrae lo stesso numero, anziché aggiungerlo.

Il secondo principio di equivalenza è simile al primo, ma riguarda le moltiplicazioni e le divisioni. Se si moltiplicano o si dividono per lo stesso numero entrambi i membri, si ottengono due disequazioni lineari equivalenti. Ad esempio,

\(\)\[x+1>6\]\(\)

è equivalente a:

\(\)\[2(x+1)>2 \cdot 6 \rightarrow 2x+2>12.\]\(\)

Oppure, con la divisione:

\(\)\[\frac{x+1}{2}>\frac{6}{2} \rightarrow \frac{x+1}{2}>3 \]\(\)

Due raccomandazioni:

1. la moltiplicazione e la divisione deve riguardare tutto il membro e non solo un termine: \(\)\[2x+1>12 \, non \, equivale \, a \, 2(x+1)>12 \]\(\)
2. non puoi dividere per 0.

Adesso, pensiamo un po’ più in grande: che succede se il numero per cui si moltiplica o si divide è negativo? Vediamolo subito con quest’esempio su un diseguaglianza:

\(\)\[4>3.\]\(\)

Moltiplicando per -1 entrambi i membri, otteniamo -4 da un lato, -3 dall’altro. Ma a questo punto il verso della disuguaglianza deve essere invertito per mantenerla vera! Quindi:

\(\)\[-4<-3.\]\(\)

Questo discorso chiaramente si estende anche per le disequazioni:

\(\)\[2x-1 \leq 5x+2 \rightarrow -2x+1 \geq -5x-2. \]\(\)

Due disequazioni lineari equivalenti hanno le stesse identiche soluzioni.

Disequazioni lineari esercizi

Come appaiono, dunque, le soluzioni di una disequazione? Facciamo alcuni esempi insieme! Riprendiamo l’ultima disequazione:

\(\)\[2x-1 \leq 5x+2 \]\(\)

Per risolverla, applichiamo i principi di equivalenza che abbiamo appena imparato, in modo tale da avere ad un solo membro la x (facciamo quello di sinistra). Quindi:

• sommiamo +1 ad ambo i lati così da annullare il -1 a sinistra:

\(\)\[2x-1+1 \leq 5x+2+1 \rightarrow 2x \leq 5x+3 \]\(\)

• sottraiamo -5x, sempre ad entrambi i membri:

\(\)\[2x-5x \leq 5x+3-5x \rightarrow -3x \leq 3 \]\(\)

• infine, dividiamo per -3 (ricordandoci di invertire il senso della disequazione):

\(\)\[\frac{-3x}{-3} \leq \frac{3}{-3} \rightarrow x \geq -1 \]\(\)

La soluzione tipica delle disequazioni lineari ha questa forma. In altre parole, per risolvere il problema possiamo considerare tutti i numeri (interi, frazioni, numeri irrazionali, cani e gatti) maggiori di -1, “-1” compreso. Cioè: -1; -0.5; 0.3450934…; 2’104’985 e così via. Esistono altri due modi per rappresentare le soluzioni. Il primo, molto più intuitivo, è tramite un grafico, cioè:

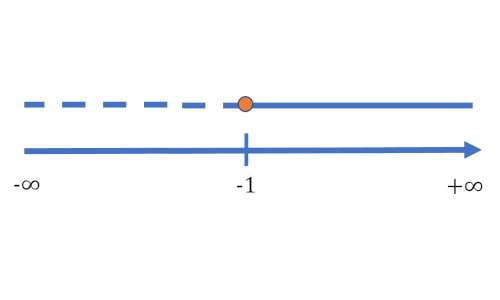
Con la linea continua si indicano i numeri inclusi nella soluzione, con quella tratteggiata quelli esclusi. Il pallino è colorato perché “-1” fa anch’esso parte delle soluzioni. Se invece fosse stato colorato di bianco, quindi vuoto, -1 non sarebbe stato incluso. L’altra possibilità, più formale, sono gli intervalli. In questo caso si utilizzano le parentesi quadre [ ] in cui si scrivono gli estremi dell’intervallo dei numeri soluzione della disequazione. Nell’esempio, sarebbe:

\(\)\[x \in [-1;+\infty[. \]\(\)

Il simbolo di appartenenza, , ci dice che la x è un numero compreso in quell’intervallo; la prima parentesi “[“, rivolta all’interno dell’intervallo, indica che -1 è compreso, mentre la seconda “[“, rivolta verso l’esterno, indica che l’infinito è escluso (e non potrebbe essere diversamente dato che  non è un numero). Più in là vedremo un altro esempio di soluzione.

DISEQUAZIONI LINEARI: DISTINGUIAMOLE

Solitamente, quando ci si trova di fronte ad una situazione che comprende più sotto casi, si creano delle categorie. In questo caso, possiamo creare due metodi di classificazione: disequazioni lineari intere e fratte; disequazioni lineari numeriche e letterali. Sono due classificazioni indipendenti, il che significa che potremmo ritrovarci a che fare con disequazioni lineari intere letterali, e altre combinazioni. In realtà, le disequazioni intere sono quelle che abbiamo già visto: sono quelle che presentano la x solo al numeratore. Quindi, anche se vi è un denominatore con solo numeri noti, siamo ancora nel caso delle disequazioni intere. Adesso, invece, vediamo gli altri casi uno ad uno.

Disequazioni lineari fratte

A differenza del caso precedente, invece, le disequazioni lineari fratte riportano l’incognita anche al denominatore, come potete vedere di seguito:

\(\)\[\frac{x+2}{x-3} < 2. \]\(\)

In questo caso, si procede portando tutto al primo membro (cioè sommando -2 come prima) e, facendo alcuni semplici conti algebrici (per i pro: il minimo comune multiplo), si ottiene:

\(\)\[\frac{x+2-2x+6}{x-3} < 0. \]\(\)

Dopo aver sommato i termini simili (incognite con incognite e numeri coi numeri), si procede come se fossero due disequazioni lineari intere, ponendo sia numeratore che denominatore maggiori di 0. Il nostro scopo è trovare quell’intervallo di valori di x che, sostituiti nella frazione, restituisca un valore negativo.

\(\)\[Num: \, -x+8 >0 \\ Den: \, x-3 >0. \]\(\)

Da cui si ricavano:

\(\)\[Num: \, x<8 \\ Den: \, x >3. \]\(\)

Queste due soluzioni significano che, affinché il numeratore e il denominatore siano positivi separatamente, la x deve essere rispettivamente <8 e >3. Come procediamo quindi? Richiamiamo il metodo grafico e scriviamo le due soluzioni, una sotto l’altra:

Adesso, visto che lì dove la linea è continua abbiamo un valore positivo, mentre la linea tratteggiata indica un valore negativo, scriviamo proprio questi due segni sopra ogni linea. Ora chiediamoci: quali sono i valori di x per cui il segno totale della disequazione fratta è negativo (come richiesto dalla traccia)? Avendo a che fare con una divisione, dalla regola dei segni sappiamo che se essi sono concordi, il segno totale sarà positivo, mentre se discordi esso sarà negativo.

Dunque, la disequazione avrà segno negativo per

\(\)\[x<3 \lor x>8, \]\(\)

che si può anche scrivere così:

\(\)\[x \in ]-\infty; 3[ \, \cup \, ]8;+\infty[, \]\(\)

dove \( \cup \) è il simbolo dell’unione di due insiemi.

Disequazioni lineari letterali

Le altre due categorie di disequazioni lineari sono quelle numeriche e quelle letterali. Le prime, però, sono quelle che contengono solo numeri (oltre alle x), e le abbiamo già viste negli esempi precedenti. Pertanto, passiamo subito a quelle letterali, che contengono cioè anche le lettere (a, b…) al posto dei numeri. Chiaramente, le disequazioni letterali si ritrovano anche nelle disequazioni lineari fratte e intere. Lanciamoci subito in un esempio:

\(\)\[(a+4)x>3. \]\(\)

In questo caso, dovremmo dividere ambo i membri per \(a+4\). Tuttavia, non sappiamo quanto valga \(a\). Dobbiamo discutere di 3 casi:

• Caso 1: \((a+4)>0 \rightarrow a>4 \). Qui possiamo procedere senza problemi ottenendo:

\(\)\[x>\frac{3}{a+4}. \]\(\)

• Caso 2: \((a+4)<0 \rightarrow a<4 \). Adesso, l’intero coefficiente di x è negativo, quindi possiamo ancora dividere ma dobbiamo anche cambiare il senso della disequazione:

\(\)\[x<\frac{3}{a+4}. \]\(\)

• Caso 3: \((a+4)=0 \rightarrow a=4 \). La disequazione qui diventa:

\(\)\[0x>3 \rightarrow 0>3, \]\(\)

il che la rende una disuguaglianza falsa.

DISEQUAZIONI LINEARI: LEVEL UP

Questo capitolo è per i più duri e interessati all’argomento. Esistono disequazioni lineari più complicate rispetto a quelle analizzate finora: vi presentiamo le disequazioni lineari goniometriche (ossia le disequazioni lineari in seno e coseno) e le disequazioni lineari in due incognite! Partiamo dalle prime.

Disequazioni lineari goniometriche

Le disequazioni lineari goniometriche contengono una funzione in seno e/o coseno, come nell’esempio seguente:

\(\)\[ \cos x > \frac{1}{2}. \]\(\)

Le disequazioni in seno e coseno le risolviamo con metodi grafici. Un metodo è guardare la funzione del coseno e cercare i valori x per cui il coseno è effettivamente più grande di ½:

In realtà, possiamo arrivare allo stesso risultato con il metodo della circonferenza goniometrica. Anziché guardare la funzione, adesso prendiamo la circonferenza, appunto, e la tagliamo alla quota di ½: selezioneremo tutti gli angoli per cui l’arco di circonferenza si troverà a una quota più alta proprio di ½.

Disequazioni lineari in due incognite

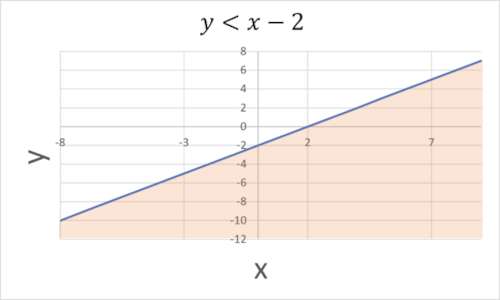
Siamo giunti finalmente al termine di questa maratona. Le disequazioni lineari in due incognite presentano le variabili x e y. Potremmo ritrovarci in una situazione del genere:

\(\)\[x-y-2 >0. \]\(\)

Non lasciatevi impaurire: è molto più semplice di quanto pensiate. Isolando la y, infatti, otteniamo un’espressione che è molto simile all’equazione di una retta:

\(\)\[y<x-2, \]\(\)

soltanto che anziché esserci il segno di uguale, c’è un segno di disuguaglianza. Aver notato che è simile a una retta ci può tornare molto utile: infatti, se   è l’insieme dei punti lungo la retta, la disequazione comprenderà tutti i punti sotto di essa!