I modelli epidemiologici sono modelli matematici costituiti da una o più equazioni che prendono in esame la genesi e l’evoluzione di un fenomeno di interesse sanitario, come ad esempio una malattia. Questi modelli sono molto utili perché possono proporre dei parametri significativi per un’analisi e una classificazione della malattia e di conseguenza per determinare le strategie migliori per diminuirne la trasmissione.
IN BREVE
Indice
MODELLI EPIDEMIOLOGICI: STORIA
Storicamente, il primo modello matematico epidemiologico per la diffusione di una malattia, venne formulato nel 1760 da Daniel Bernoulli, con lo scopo di supportare la vaiolizzazione, ovvero la vaccinazione contro il vaiolo; questo modello mostrava che, tramite l’inoculazione di materiale prelevato da lesioni vaiolose o dalle croste di pazienti non gravi, l’aspettativa di vita sarebbe aumentata da 26 anni e 7 mesi a 29 anni e 9 mesi. Il primo a introdurre una teoria matematica delle epidemie fu William Farr nel 1865, descrivendo e riuscendo a predire l’andamento della peste bovina mediante un’equazione polinomiale di terzo grado. Farr, che studiò medicina e statistica e fu allievo di Thomas R. Malthus, formulò la correlazione tra malattie e povertà urbana e elaborò una tassonomia delle malattie. L’uso di modelli matematici epidemiologici nell’analisi della diffusione delle malattie infettive si è largamente diffuso a partire dal ventesimo secolo. All’inizio del ‘900 vennero proposti dei modelli a tempi discreti da parte di John Brownlee e William H. Hamer, quest’ultimo ipotizzò che la diffusione delle epidemie dipendesse dal tasso di contatto tra individui suscettibili e che il tasso di diffusione dell’infezione fosse proporzionale al prodotto della densità di persone suscettibili (individui sani passibili di contagio) e la densità di individui infetti, noto come principio dell’azione di massa. Considerando questo principio, William O. Kermack e Anderson G. McKendrick proposero un modello di tipo differenziale (SIR) per spiegare la crescita e la decrescita del numero di persone infette, osservate in alcune epidemie di peste (nel 1665-1666 a Londra, nel 1906 a Bombay) e di colera (nel 1865 a Londra). Per questo modello enunciarono la teoria della soglia, secondo la quale un numero esiguo di individui infetti in una comunità di individui suscettibili darà origine ad una pandemia se la densità o il numero di individui suscettibili è al di sopra di un determinato valore critico (\( \sigma \)); quindi, se \( \sigma > 1 \) la malattia riesce a diffondersi all’interno della popolazione, invece se \( \sigma \leq 1 \) la malattia decade a zero senza diffondersi in maniera estesa nella popolazione. Da questo modello SIR ne sono derivati numerosi altri con l’aggiunta di altre variabili. Nel 1910 il medico tropicale Ronald Ross propose il primo modello probabilistico correlando l’incidenza della malaria al numero di zanzare. Successivamente George Macdonald, tramite il modello di Ross, ricavò il concetto di tasso di riproduzione dell’infezione \( R_0 \), che rappresenta il numero di infezioni secondarie causate da un singolo caso di organismo infetto. Successivamente questo indice è stato utilizzato nell’ambito di modelli stocastici per caratterizzare le dinamiche di diffusione delle malattie infettive dal punto di vista quantitativo; affinché la malattia infettiva si propaghi all’interno di una popolazione, l’indice \( R_0 \) deve essere maggiore di 1, ovvero ogni ospite infettato deve trovarsi in un ambiente che possa facilitare contatti con organismi suscettibili. Negli anni ’20 del Novecento Lowell Reed e Wade H. Frost inquadrarono i fattori spaziali e temporali che caratterizzano il diffondersi di una malattia e l’intensità di una epidemia nel modello epidemico Reed-Frost: la propagazione della malattia varia in relazione alla probabilità di contatti infettivi e ospiti suscettibili. I fattori che possono influenzare la probabilità sono: la densità di popolazione, la suscettibilità e l’infettività, la trasmissibilità, la durata del tempo di contatto e la virulenza dell’agente infettivo. Negli ultimi decenni sono stati elaborati modelli matematici sempre più complessi e sofisticati che cercano di analizzare le dinamiche delle forme epidemiche che caratterizzano le diverse malattie infettive.

TIPOLOGIE DI MODELLI EPIDEMIOLOGICI
La distinzione principale avviene tra modelli deterministici e modelli stocastici. I modelli deterministici sono i più semplici: le variabili in input assumono dei valori già determinati e gli individui della popolazione vengono divisi in gruppi, ogni gruppo rappresenta uno stadio specifico dell’epidemia. Questo tipo di modello viene utilizzato quando si hanno popolazioni vaste e viene elaborato utilizzando equazioni differenziali, dal momento che i tassi di transizione da un gruppo ad un altro vengono espressi come derivate. I modelli stocastici invece in input tengono in considerazione la variazione delle variabili e forniscono in output dei risultati probabilistici. Questi modelli permettono di stimare le distribuzioni di probabilità variando i parametri in input a seconda della malattia in esame e, per questo motivo, avendo una struttura più complessa, riescono ad essere più aderenti alla realtà.
Numero di riproduzione di base, \( R_0 \)
Una caratteristica importante per i modelli epidemiologici è il numero di riproduzione di base, \( R_0 \), ovvero il numero atteso di nuovi casi generati, in media, da un caso singolo durante il suo periodo infettivo all’interno di una popolazione in cui tutti gli individui sono suscettibili all’infezione. Questo valore viene utilizzato per molteplici scopi: determinare se una malattia infettiva può diffondersi in una popolazione, prevedere il numero di contagiati durante un’epidemia, determinare quale percentuale della popolazione debba essere vaccinata per immunizzarsi per debellare una malattia. Nei modelli di infezione più utilizzati se \( R_0 < 1 \), ogni persona infetta in media meno di una persona e quindi l’infezione a lungo termine andrà a scomparire; se \( R_0 > 1 \), in media ogni persona infetta un’altra persona e quindi la malattia si diffonderà; se \( R_0 = 1 \) ogni persona infetta in media esattamente un’altra persona e quindi la malattia diventa endemica, ovvero si sposterà in tutta la popolazione senza aumentare o diminuire. In un modello semplificato e con un vaccino efficace al 100%, per prevenire la diffusione dell’infezione, la popolazione che deve immunizzarsi deve essere pari a \( 1- \frac{1}{R_0} \). Le stime per il calcolo del valore di \( R_0 \) per le malattie infettive, le cui variabilità possono essere molto ampie, spesso tengono conto di tre parametri: la durata della contagiosità di una persona, la probabilità di infezione per contatto tra due individui, il tasso di contatto. Esiste un caso particolare in cui questo parametro può essere calcolato senza ricorrere alle equazioni differenziali: quando la malattia infettiva è endemica, ovvero quando un individuo ne infetta esattamente un altro. Matematicamente parlando ciò avviene se \( R_0 \cdot S =1 \), dove \( S \) è la quantità di suscettibili rispetto alla popolazione totale. In una popolazione con piramide dell’età rettangolare se si suppone che ogni individuo abbia la stessa aspettativa di vita, che le persone più giovani siano sensibili e le persone più anziane siano già state immunizzate da una infezione precedente, la percentuale degli infettabili risulta essere $$ S=\frac{A}{L} $$ con \( L \) età media della popolazione ed \( A \) età media degli infettati. Nel caso di malattia infettiva endemica vale anche che \( S=\frac{1}{R_0} \) , quindi $$ R_0 = \frac{L}{A} $$
Se invece si assume che la piramide dell’età sia esponenziale, si usano modelli di equazioni differenziali ordinarie per ricavare l’equilibrio endemico e di ottiene: $$ R_0 = 1+ \frac{L}{A} $$
Di solito, nelle prime fasi, l’epidemia cresce in modo esponenziale, con un tasso logaritmico pari a $$ K=\frac{d\ln(P)}{dt} $$ dove \( P \) può essere interpretato come il numero di pazienti positivi attuale. Per stimare \( R_0 \) sono necessarie ulteriori informazioni e per rendere il modello più realistico bisogna assumere misure di contenimento e quindi altri parametri: un individuo infetto asintomatico e che non infetta ancora gli altri rientra nel gruppo \( E \), la durata dello stato esposto è \( \tau_E \); un individuo infetto asintomatico che infetta gli altri rientra nel gruppo \( I \), la durata dello stato infettivo latente è \( \tau_I \); gli individui isolati rientrano nel gruppo \( R \). In questo caso, usando un modello SEIR, \( R_0 \) può essere scritto: $$ R_0 = 1 + K(\tau_E + \tau_I) + K^2 \tau_E\tau_I $$

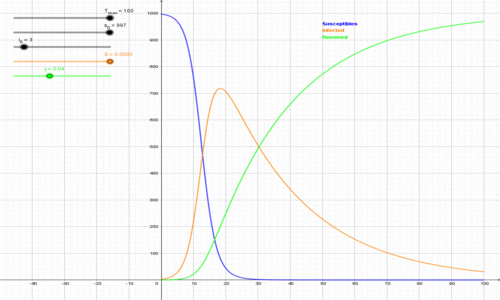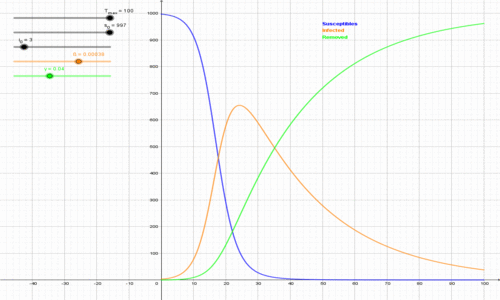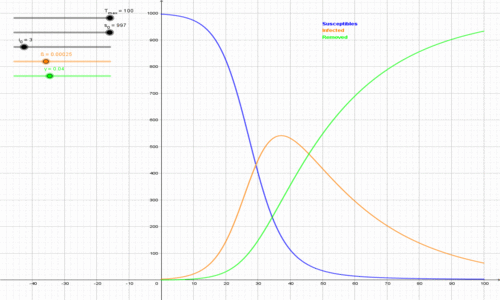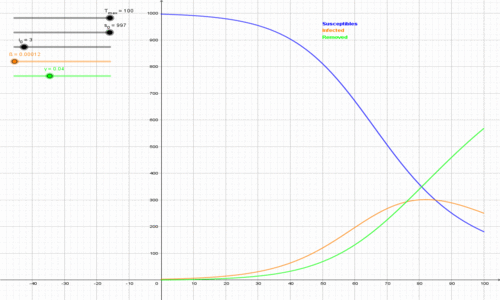
Blu=suscettibili
Celeste=infetti
Marrone=recuperati (Credit: Wikimedia – Beta212, creata con python, ridimensionata, ritagliata, dimensioni: 500×300 px, Attribuzione – Condividi allo stesso modo 3.0 Unported (CC BY-SA 3.0)).
Numero di riproduzione al tempo \( t \), \( R_t \)
La definizione del numero di riproduzione al tempo t, \( R_t \), è analoga a quella di \( R_0 \). L’indice \( R_t \) viene calcolato in un preciso istante di tempo e la sua variazione permette di monitorare l’andamento di un’epidemia e anche i mezzi da utilizzare per contrastarla. La stima di questo parametro viene fatta mediante calcoli statistici applicati al modello matematico che meglio descrive l’andamento dell’epidemia. Esistono due definizioni principali dell’\(R_t\), \( R_{t(istantaneo)} \) e \( R_{t(caso)} \): Il primo è il numero medio di casi secondari che ogni individuo infetto infetterebbe se le condizioni non variassero rispetto a quelle del tempo \( t \) e può essere stimato tramite il rapporto tra il nuovo numero di infezioni e la contagiosità totale al tempo \( t \) (\( w_s \)); il secondo è il numero medio di casi secondari che un caso infettato al tempo \( t \) finirà per infettare e può essere calcolato solamente a posteriori. Sono stati sviluppati nel tempo diversi metodi di calcolo per il parametro \( R_t \), basati nella maggior parte dei casi su modelli SEIR e una delle formule più utilizzate è la seguente: $$ R_t = \frac{I_t}{\sum_{s=1}^t w_s I_{t-s}} $$ dove \( I_t \) è il numero di infezioni avvenute il giorno \( t \) e \( w_s \) è la probabilità che si abbiano \( s \) giorni tra quando un individuo viene contagiato e infetta un nuovo individuo. Nel corso dell’epidemia di COVID-19, l’ISS nel calcolo di questo parametro si basa sull’utilizzo del metodo Monte Carlo su catena di Markov. Dopo un certo numero di iterazioni, l’algoritmo converge verso la distribuzione che meglio descrive l’evoluzione dell’epidemia virale. A tale obiettivo l’algoritmo viene applicato alla seguente funzione di verosimiglianza: $$ L=\prod_{t=1}^T P(C_t-Imp_t|R_t\sum_{s=1}^t w_s C_{t-s}) $$ con \( P(k|\lambda) \) è la densità di una distribuzione di Poisson, \( C_t \) è il numero di casi sintomatici con data di inizio dei sintomi al giorno \( t \), \( Imp_t \) è il numero di casi sintomatici importati da altre regioni o dall’estero con i sintomi iniziati al giorno \( t \).
MODELLI COMPORTAMENTALI
Nei modelli epidemiologici per semplificare le simulazioni si assume che la popolazione sia divisa in compartimenti e che tutti gli individui in un determinato compartimento abbiano le stesse caratteristiche. Questi modelli possono essere utilizzati per prevedere l’andamento di un’epidemia o la sua durata, per comprendere la percentuale di vaccinazioni necessaria per procurare l’immunità di gregge. La gran parte dei modelli utilizzati attualmente hanno origine dal modello proposto da Kermak e McKendrick nel 1927 e permettono di classificare la popolazione \( N \) in compartimenti, i più comuni sono:
- \( S \), suscettibili;
- \( I \), infetti/infettivi;
- \( E \), esposti, individui infetti non ancora infettivi;
- \( R \), recuperati, guariti, non infettabili perché resi immuni dopo aver contratto la malattia.
Si può studiare la dinamica anche inserendo ulteriori sotto-compartimenti a seconda della fascia d’età ed esistono modelli più accurati con altre classificazioni che tengono conto, per esempio, dei vaccinati, dei soggetti in quarantena e degli asintomatici. I modelli più semplici per simulare la dinamica al tempo \( t \) di un’epidemia utilizzano come parametri:
- \( S_{(t)} \), numero di suscettibili al giorno \( t \);
- \( I_{(t)} \), numero di infetti/infettivi al giorno \( t \);
- \( E_{(t)} \), numero di esposti, individui infetti non ancora infettivi al giorno \( t \);
- \( R_{(t)} \), numero di guariti al giorno \( t \).
Nei modelli dove vale \( N_{(t)} = S_{(t)} + E_{(t)} + I_{(t)} + R_{(t)} \), \( R_{(t)} \) può includere immuni, isolati, deceduti e persone in quarantena.
La maggior parte dei modelli viene denominata con un acronimo che rappresenta il flusso dell’epidemia nei diversi compartimenti:
- SI: \( S \Longrightarrow I \)
- SIS: \( S \Longrightarrow I \Longrightarrow S \)
- SIR: \( S \Longrightarrow I \Longrightarrow R \)
- SEIR: \( S \Longrightarrow E \Longrightarrow I \Longrightarrow R \)
I modelli possono adattarsi a malattie sia nella fase endemica che epidemica, a sistema aperto (che considera anche nascite e decessi) o chiuso. Per lo sviluppo dei modelli sono necessari anche dei parametri: il tasso di infezione o velocità di trasmissione del virus, \( \beta \), il cui reciproco indica il tempo medio tra i contatti; il tasso di recupero, \( \gamma \), il cui reciproco indica il tempo infettivo medio; il tasso di incubazione, \( \alpha \), il cui reciproco indica il tempo medio di incubazione. Possono essere inseriti ulteriori parametri per rendere il modello più accurato. Inoltre se viene inserito il tasso di letalità (CFR) e il tempo che intercorre tra la diagnosi e il decesso, si può stimare il numero di morti provocati dall’epidemia; se si varia il parametro \( R_0 \) si può stimare l’effetto delle misure di contenimento utilizzate; se si inserisce il tasso di ospedalizzazione e il numero medio di ricoverati è possibile prevedere la pressione sulle strutture sanitarie.
Modello SI
Il modello più semplice di diffusione di una malattia presuppone che la popolazione sia divisa in due compartimenti, infetti e suscettibili. Se si indica con \( S=S(t) \) e con \( I = I(t) \) il numero di suscettibili e il numero di infetti al tempo \( t \), se \( N=N(t) \) indica la popolazione totale, \( s=\frac{S}{N} \) e \( i=\frac{I}{N} \) indicano le frazioni di suscettibili e infetti rispetto alla popolazione totale. Considerando la legge di azione di massa si può porre \(\Delta I \approx \lambda I S \Delta t \), con \( \lambda \) costante. Tuttavia questa scelta non concorda con i dati osservati, quindi si utilizza la relazione di incidenza standard: $$ \Delta I \approx \beta \frac{I}{N} S \Delta t = \beta i S \Delta t$$ con \( \beta \) numero medio di contatti a persona sufficienti per trasmettere la malattia per unità di tempo. L’identità tra il primo termine e l’ultimo vale solo nel senso della legge dei grandi numeri. Facendo tendere \( \Delta t \) a \( 0 \) e considerando quanto detto finora, le equazioni che descrivono il modello sono le seguenti:
$$ \frac{ds}{dt} = -\beta s i, \,\,\,\,\, \,\,\,\,\, \,\,\,\,\, \frac{di}{dt} = \beta s i $$
La popolazione totale si conserva nel tempo, quindi \( s(i) + i(t) =1 \). Risolvendo le equazioni è possibile trovare l’espressione analitica per \( S(t) \) e per \( I(t) \):
$$ S(t) = \frac{ N S_0}{S_0 + I_0 e^{\beta t}}, \,\,\,\,\, \,\,\,\,\, \,\,\,\,\, I(t) = \frac{ N I_0 e^{\beta t}}{S_0 + I_0 e^{\beta t}}$$
dove \( S_0 \) e \( I_0 \) sono rispettivamente gli individui suscettibili e infetti al tempo 0. Se si studia il comportamento asintotico di queste due soluzioni (per \( t \rightarrow +\infty \) si può vedere che \( S(t) \rightarrow 0 \) e \( I(t) \rightarrow +\infty \), ovvero la malattia è destinata a diffondersi in tutta la popolazione. La curva epidemica, la curva che analizza il tasso di crescita degli infetti ha la seguente forma:
$$ \frac{di}{dt} =\frac{\beta s_0 i_0 e^{\beta t}}{(s_0+i_0 e^{\beta t})^2} $$
e presenta un massimo in \( t=\ln(\frac{s_0}{i_0})/\beta \).
Modello SIS
Il modello SIS descrive il caso di malattie da cui si guarisce, ma che non danno immunità, ad esempio il raffreddore. Supponendo che la durata della malattia sia \( \frac{1}{\gamma} \), la diffusione della malattia è formulata sotto forma di equazioni differenziali ordinarie:
$$ \frac{ds}{dt} = -\beta s i + \gamma i, \,\,\,\,\, \,\,\,\,\, \,\,\,\,\, \frac{di}{dt} = \beta s i – \gamma i $$
dove \( – \beta s i \) indica il tasso di movimento dalla categoria dei suscettibili a quella degli infetti e \( – \gamma i \) il tasso a cui gli infetti guariscono e tornano nella categoria dei suscettibili. La popolazione totale si conserva nel tempo, quindi \( s(i) + i(t) =1 \). Le soluzioni che si ottengono sono:
$$ s(\tau) = \frac{ s_0 +(1-s_0)\tau}{1+(1-s_0)\tau}, \,\,\,\,\, \,\,\,\,\, \,\,\,\,\, i(\tau) = 1-s(\tau)=\frac{ i_0}{1+i_0\tau } $$
dove \( \tau := \beta t \). Se si pone \( \sigma := \frac{\beta}{\gamma} \), chiamato numero di contatto, ovvero il prodotto tra il tasso di contatto e il tempo media di durata della malattia, e si studia il comportamento asintotico di \( i(\tau) \) nei casi in cui \( \sigma \leq 1 \) e \( \sigma > 1 \) si ottiene:
$$ \lim_{t \rightarrow +\infty} i(t)=
\bigg \{
\begin{array}{rl}
& 0 &\sigma \leq 1\\
& 1-\frac{1}{\sigma} &\sigma > 1 \\
\end{array}
$$
A seconda del valore del parametro si ha l’estinguersi del processo o la propagazione a tutta la popolazione.
Modello SIR
Il modello SIR inserisce la possibilità che gli infetti vengano rimossi dalla circolazione conseguentemente a una guarigione (il termine del periodo di infettività), all’acquisizione dell’immunità, all’isolamento o al decesso. Gli individui infetti vanno ad accrescere il compartimento dei rimossi. Questo modello viene utilizzato per le malattie infettive come morbillo, parotite o rosolia, che vengono trasmesse da uomo a uomo e il recupero conferisce resistenza duratura. Le equazioni differenziali che descrivono il modello sono le seguenti:
$$ \frac{ds}{dt} = -\beta s i, \,\,\,\,\, \,\,\,\,\,\frac{di}{dt} = \beta s i – \gamma i \,\,\,\,\, \,\,\,\,\, \frac{dr}{dt}=\gamma i $$
Anche in questo caso \( s(i)+i(i)+r(i) =1 \) e l’andamento della soluzione dipende anche questa volta dal parametro \( \sigma \). Le prime due equazioni differenziali sono disaccoppiate dalla terza e possono essere svolte separatamente. Si può supporre per semplicità che \( r_0=0 \) e quindi \( s_0+i_0 =1 \). Dalle due equazioni si deduce:
$$ \frac{di}{ds}=\frac{di/dt}{ds/dt}= -1+\frac{1}{\sigma s} $$
Quindi l’espressione di \( i \) risulta essere:
$$ i=1-s-\frac{1}{\sigma}\ln(\frac{s_0}{s}) $$
Se \( \sigma \leq 1 \) sia \( s \) che \( i \) sono decrescenti nel tempo; se \( \sigma > 1 \) vi sono due eventualità: se \( s_0 \leq \frac{1}{\sigma} \) il comportamento è simile al caso precedente (infatti se \( S(t) < \frac{1}{\sigma} \Rightarrow \frac{dI}{dt} <0) \), se \( s_0 > \frac{1}{\sigma} \) la funzione \( i(t) \) aumenta fino al valore massimo \( i_{max}= 1-[1+\ln(\sigma s_0)]/\sigma\) e poi decresce a zero per \( t \rightarrow +\infty \).
Modello SEIR
Per molte malattie infettive esiste un periodo di tempo, periodo di incubazione, in cui gli individui sono stati infettati ma non sono ancora infettivi. Questi soggetti rientrano nella categoria esposti. Questo modello viene descritto dalle seguenti equazioni differenziali:
$$ \begin{array}{rl} &\frac{ds}{dt} = -\beta s i, \,\,\,\,\, \,\,\,\,\, \,\,\,\,\, &\frac{de}{dt} = \beta s i – \epsilon e, \\
&\frac{di}{dt}=\epsilon e-\gamma i, \,\,\,\,\, \,\,\,\,\, \,\,\,\,\, &\frac{dr}{dt} = \gamma i, \end{array}$$
dove \( \epsilon \) è il periodo che intercorre tra quando l’individuo è stato contagiato e quando diventa a sua volta contagioso. Se si aggiunge il parametro \( \delta \) che rappresenta coefficiente di natalità/mortalità, il sistema diviene:
$$ \begin{array}{rl} &\frac{ds}{dt} = -\beta s i+\delta-\delta s, \,\,\,\,\, \,\,\,\,\, \,\,\,\,\, &\frac{de}{dt} = \beta s i – (\epsilon + \delta)e, \\
&\frac{di}{dt}=\epsilon e-(\gamma+\delta)i, \,\,\,\,\, \,\,\,\,\, \,\,\,\,\, &\frac{dr}{dt} = \gamma i –\delta r. \end{array}$$
Nel primo caso \( \sigma = \frac{\beta}{\gamma} \) e nel secondo \( \sigma = \frac{\beta\epsilon}{(\gamma+\delta)(\epsilon+\delta)} \). La soluzione del problema \( (s,e,i,r) \) dipende dal valore assunto da \( \sigma \): se \( \sigma \leq 1 \), le traiettorie convergono all’equilibrio \( (1,0,0,0) \), se \( \sigma > 1 \), tutte le soluzioni con \( i_0 >0 \) convergono all’equilibrio \( (s_e,e_e,i_e,r_e) \), dove
$$ (s_e,e_e,i_e,r_e) =\biggl(\frac{1}{\sigma}, \frac{\sigma}{\epsilon+\sigma} \biggl(1-\frac{1}{\sigma}\biggr), \frac{\delta(\sigma-1)}{\beta},\frac{\gamma(\sigma-1)}{\beta}\biggr).$$
Fonte
- Modelli deterministici in epidemiologia
Modelli deterministici in epidemiologia - A contribution to the mathematical theory of epidemics
The Royal Society - Modeling epidemics with differential equations
Tennessee State Univeristy Internal Report - The Mathematics of Infectious Diseases
SIAM









