Ponte di Tacoma: un crollo che ha fatto la storia

LA STRUTTURA DEL PONTE

Il crollo del ponte di Tacoma ha rappresentato un evento significativo a scala mondiale. Questo non dipende soltanto dagli impressionanti video che circolano tutt’ora in rete, ma anche e soprattutto per il peso che ha avuto sugli studi successivi. Il caso del ponte infatti, è stato ampiamente analizzato permettendo la comprensione di alcuni fenomeni fisici e lo sviluppo di nuove tecnologie in campo ingegneristico.

Costruzione del ponte di Tacoma

Il ponte di Tacoma Narrow fu costruito in negli Stati Uniti, sul canale di Puget, per collegare la Olympic Peninsula allo stato di Washington. Inaugurato nel luglio del 1940, era al tempo il terzo ponte più lungo al mondo raggiungendo 1524 metri di estensione. A causa del budget limitato il ponte fu costruito come struttura sospesa. I ponti sospesi sono costituiti da un impalcato, due torri, due funi e da una serie di barre che connettono le funi alla piattaforma. Il vantaggio principale di questo tipo di costruzioni è la possibilità di coprire distanze molto grandi con solo due torri, riducendo costi e materiali. Per l’impalcato del ponte di Tacoma gli ingegneri optarono per un’innovativa soletta in calcestruzzo armato irrigidita da due travi longitudinali a doppia T poste ai lati della struttura. Queste ultime, andando a sostituire la convenzionale struttura reticolare, diedero al ponte una forma affusolata, facendogli guadagnare l’appellativo di narrow, sottile.

Primi problemi

Durante le fasi finali del lavoro di costruzione del ponte di Tacoma iniziarono a verificarsi i primi problemi strutturali con l’insorgere di insolite oscillazioni verticali. Il ponte era così flessibile sotto l’azione dei venti da nauseare gli operai del cantiere. Per questo motivo furono installati cavi obliqui tra le funi e l’impalcato per aumentare la rigidezza verticale e torsionale del ponte. Nonostante gli interventi, le ondulazioni del ponte continuarono anche dopo l’inaugurazione, facendo guadagnare al ponte l’appellativo di Gallopping Gertie. Queste particolari oscillazioni attirarono l’interesse degli automobilisti che nell’attraversare il ponte osservavano i veicoli che li procedevano scomparire nella depressione di un’onda. Preoccupati da questi insoliti movimenti, gli ingegneri installarono dispositivi in grado di monitorare la direzione e la velocità del vento e correlarla alla risposta strutturale. Tuttavia, questo non fu sufficiente per impedire il drammatico crollo.

CROLLO DEL PONTE DI TACOMA

Il 7 novembre del 1940, a soli quattro mesi dall’inaugurazione, crollò la campata centrale del Ponte di Tacoma Narrows a causa delle vibrazioni indotte dal vento. Quel giorno, oltre alle solite oscillazioni verticali, si innescarono sul ponte oscillazioni torsionali, mai osservate prima. Questi violenti movimenti provocarono la rottura dei cavi di sospensione ed il conseguente collasso.

Gli studi sul del crollo furono effettuati da una commissione formata dalla Federal Works Agency, la quale concordò che le cause del disastro erano attribuibili a difetti al materiale di costruzione, ad effetti generati dalla turbolenza e dalla velocità del vento e infine, alla mancanza di aerodinamica. Il ponte infatti era troppo deformabile a flessione e a torsione e di conseguenza era molto sensibile all’azione del vento. L’ingegnere italiano Giulio Krall fu il primo ad indicare una spiegazione tecnica più dettagliata del crollo, individuando le cause delle diverse oscillazioni. Le vibrazioni verticali furono ricondotte al fenomeno di risonanza mentre quelle torsionali alle cosiddette oscillazioni autoindotte.

Il fenomeno di risonanza

La risonanza è un fenomeno fisico che si manifesta quando la frequenza della forza eccitante eguaglia la frequenza naturale del sistema oscillante producendo un amplificarsi delle vibrazioni del sistema stesso. Per spiegare questo fenomeno possiamo prendere ad esempio le altalene: piccole e periodiche spinte all’altalena possono provocare grandi oscillazioni del sistema. Questo avviene solo quando le perturbazioni indotte dalla forza spingente, hanno una frequenza uguale a quella naturale della struttura. Ogni corpo ha infatti una frequenza naturale dipendente dalle proprie caratteristiche fisiche. Se la frequenza del moto forzato è vicina alla frequenza propria del sistema, quest’ultimo può produrre enormi ampiezze di oscillazione. Schematicamente il ponte può essere paragonato ad un oscillatore armonico forzato e smorzato. La forza esterna si può esprimere attraverso un fattore sinusoidale del tipo \(F_m\cos \left ( \omega t \right )⁡\) in cui il termine ω indica la pulsazione della sollecitazione forzante. Dalle leggi della dinamica si può ricavare la seguente equazione del moto:
\(\frac{\mathrm{d^2} x}{\mathrm{d} t^2} + b \frac{\mathrm{d} x}{\mathrm{d} t} + kx= F_m \cos \left ( \omega t \right )\)
Dove m rappresenta la massa, b il coefficiente di smorzamento e k la costante elastica. La soluzione dell’equazione differenziale risolve il moto in funzione di due parametri \(ω_0\) e  ω, dove \(ω_0\), funzione delle costanti m, b, k, è la frequenza propria di oscillazione del corpo.

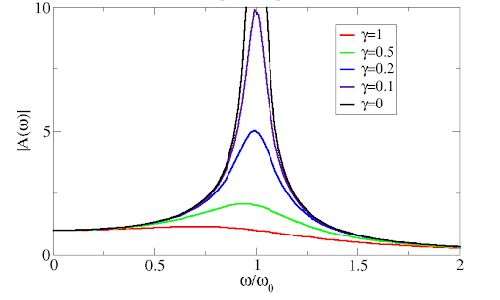
Quello che si deduce, come avevamo preannunciato, è che ci sono frequenze di sollecitazione esterna per le quali il moto si amplifica notevolmente; queste frequenze sono vicine all’oscillazione propria del sistema e sono dette frequenze di risonanza. Tornando al ponte, possiamo considerare il vento come forza motrice, la viscosità dell’aria come fattore smorzante e la rigidità strutturale come costante elastica. Quando la frequenza del vento che soffia sul ponte approssima la frequenza naturale della struttura, si innescano le ampie oscillazioni verticali che lo hanno reso noto.

Oscillazioni torsionali e crollo

I motivi per cui si sono innescate le oscillazioni di tipo torsionale non sono del tutto chiari ma l’ipotesi più ragionevole è che abbiano a che fare con l’aerodinamica del ponte. Infatti, l’estrema flessibilità, la snellezza e la leggerezza hanno favorito l’aumento delle oscillazioni. A differenza del fenomeno di risonanza, in questo tipo di oscillazioni, la forzante non è esterna ma dipende dal moto del sistema. Questo fenomeno di instabilità è chiamato aeroelastic flutter (oscillazione aeroelastica). Consiste in una vibrazione aeroelastica autoeccitata che si verifica in determinate condizioni di moto relativo tra una struttura ed il fluido in cui è immerso. Detto più semplicemente, il moto di un fluido può provocare il moto di un sistema che inizia ad oscillare con ampiezza, velocità e accelerazione crescenti nel tempo. Questo comporta un aumento dell’energia cinetica del corpo che, se supera l’energia che la struttura è in grado di assorbire, provoca la rottura del sistema. L’energia trasferita dal fluido alla struttura risulta maggiore di quella dissipata e può condurre quindi al collasso della struttura se le tensioni che si raggiungono superano i valori di resistenza del materiale. I movimenti torsionali del ponte di Tacoma sono stati provocati dal vento che, soffiando in direzione non ortogonale alla struttura, sollevava e abbassava alternatamente i lati del ponte. Ad ogni movimento torsionale si creavano vortici e aree di bassa pressione dal lato opposto a quello del moto, che amplificavano il movimento. Nel momento in cui il ponte ritornava nella posizione naturale di equilibrio, la struttura ruotava nell’altra direzione, continuando il ciclo. Le oscillazioni raggiunsero angoli superiori ai 45° rispetto all’orizzontale, causando la rottura di uno dei cavi di sostegno ed il conseguente collasso.

Distacco di vortici e scia di Von Karman

Come abbiamo visto, il crollo del ponte è stato innescato dalle oscillazioni torsionali che hanno rotto i cavi di sospensione. Ma cosa ha generato questi movimenti? Il fenomeno di vibrazione aeroelastica si presenta in particolari condizioni di interazione tra fluido e struttura. In generale un corpo immerso in una corrente fluida può modificare le linee di flusso della corrente. L’andamento del flusso viene descritto in fluidodinamica da un valore adimensionale, il numero di Reynolds \( \left (R_e \right )\), proporzionale alla velocità, alla densità e alla viscosità del fluido. Per valori \( R_e \) compresi tra 30 e 5000 il flusso diventa instabile, generando una scia di vortici che si distaccano in modo alternato dal corpo. A valle del corpo si crea così una scia turbolenta chiamata scia Von Karman dal nome dello scienziato che per primo osservò questo fenomeno. Tale distacco di vortici non dipende soltanto dalle caratteristiche del fluido ma anche dalla forma della sezione trasversale al flusso. Ritornando al caso del ponte di Tacoma, in corrispondenza della sezione longitudinale il flusso passò da regime stazionario a turbolento. Conseguentemente si formarono vortici di Von Karman che innescarono vibrazioni aeroelastiche autoeccitate.

LA LEZIONE DEL PONTE DI TACOMA

Il caso del crollo del Ponte di Tacoma ha avuto grande risonanza all’interno del mondo accademico. Infatti, ha favorito numerosi studi per il miglioramento dell’aerodinamica delle grandi strutture e la messa a punto di nuove tecnologie di monitoraggio. Un modo con cui i moderni ponti risolvono il problema delle oscillazioni consiste nella creazione di fessure al centro della piattaforma. Un altro modo è quello di affidare la funzione portante ai cavi di sospensione, come nel caso dei ponti strallati. Inoltre le basi vengono progettate con forme maggiormente aerodinamiche per evitare la creazione di vortici. Oltre agli sviluppi formali gli esperti hanno sviluppato sistemi di simulazione come le gallerie del vento, per testare i progetti prima della costruzione. In questi impianti vengono ricreate le condizioni di vento che poi andranno ad agire sui modelli in scala delle strutture.