Equazioni goniometriche elementari: risoluzione

EQUAZIONI GONIOMETRICHE ELEMENTARI: QUALI SONO?

Le equazioni goniometriche elementari sono particolari equazioni goniometriche in cui l’incognita, che si trova all’interno dell’argomento di una funzione goniometrica si trova con coefficiente e grado pari ad \( 1 \). Per risolvere le equazioni goniometriche elementari è utile conoscere i valori delle funzioni goniometriche di angoli particolari, ovvero 30°, 45°, 60° \( (\frac{\pi}{6}, \frac{\pi}{4}, \frac{\pi}{3}) \), e dei loro multipli. Le equazioni goniometriche elementari si presentano nella seguente forma:
$$ \sin x=a \,\,\,\,\, \cos x=b $$
$$ \tan x=c \,\,\,\,\, \cos x=d $$
$$ \sec x=m \,\,\,\,\, \csc x=n. $$

Equazioni goniometriche del tipo \( \sin x=a \) o \( \cos x=b \)

Per risolvere equazioni goniometriche elementari del tipo \( \sin x=a \) o \( \cos x=b \) è necessario ricordare come sono definiti il seno e il coseno di un angolo. Il coseno di un angolo rappresenta l’ascissa (\( b \)) del punto che individua tale angolo sulla circonferenza goniometrica, mentre il seno di un angolo ne rappresenta l’ordinata (\( a \)). Quindi per risolvere un’equazione si devono individuare i punti, e quindi gli angoli, sulla circonferenza goniometrica che corrispondono all’ascissa pari a \( b \) oppure o all’ordinata \( a \), a seconda dell’equazione considerata. Nella risoluzione di un’equazione è necessario disegnare la circonferenza goniometrica e tracciare, a seconda dell’equazione, una retta del tipo \( x=b \) o \( y=a \); i punti di intersezione tra la retta e la circonferenza goniometrica sono le soluzioni cercate. In generale le equazioni goniometriche in seno e coseno ammettono soluzione solamente se \( -1 \leq a \leq 1 \) o se \( -1 \leq b \leq 1 \) poiché il seno e il coseno sono funzioni goniometriche limitate e comprese tra \( -1 \) e \( 1 \) e la retta menzionata sopra è esterna alla circonferenza goniometrica e pertanto non la interseca in alcun punto. Quindi, se \( a < -1 \vee a>1 \) oppure se \( b < -1 \vee b>1 \) l’equazione non ha soluzione; ad esempio, l’equazione
$$\sin x= -2 $$
non ha soluzione, pertanto è impossibile.

Esempio di risoluzione di un’equazione goniometrica elementare del tipo \( \cos x=b \)

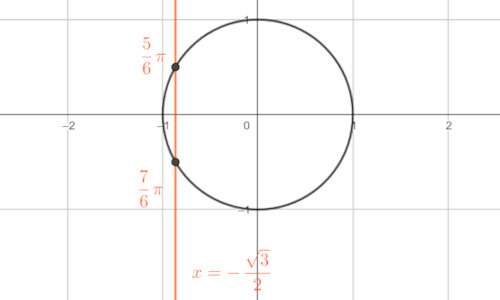
Si consideri l’equazione goniometrica \( \cos x = – \frac{\sqrt{3}}{2} \). Per risolverla l’obiettivo è trovare i punti della circonferenza goniometrica che abbiano l’ascissa pari a \( – \frac{\sqrt{3}}{2} \). Per fare ciò, si disegna la circonferenza goniometrica (ovvero una circonferenza centrata nell’origine degli assi con raggio pari a \( 1 \)) e successivamente si traccia una retta del tipo \( x=- \frac{\sqrt{3}}{2} \) e si trovano i punti di intersezione che rappresentano la soluzione cercata. La retta interseca la circonferenza in due punti, che corrispondono a due angoli: \( \frac{5}{6} \pi \) e \( \frac{7}{6} \pi \). Quindi l’equazione è soddisfatta per
$$ x= \frac{5}{6} \pi + 2k\pi \,\,\, \vee x= \frac{7}{6} \pi + 2k\pi . $$
Le soluzioni sono infinte al variare di \( k \in \mathbb{Z} \); il numero \( k \) è utilizzato per individuare tutte le possibili soluzioni tenendo conto della periodicità della funzione di \( 2\pi \).

Alternativamente per determinare le soluzioni di una equazione del tipo \( \cos x=b \) si può procedere nel seguente modo:

• Se \( b \) è un valore noto, ovvero corrisponde a un multiplo di 30°, 45°, 60°, indicando con \( \beta \) l’angolo del primo quadrante che soddisfa l’equazione \( \cos \beta=b \), le soluzioni saranno del tipo:$$ x= \beta + 2k\pi \,\,\, \vee x= (2\pi – \beta) + 2k\pi \,\,\,\, k \in \mathbb{Z}; $$
•  Se \( b \) non è un valore noto, le soluzioni saranno del tipo:
  $$ x= \arccos b + 2k\pi \,\,\, \vee x= (2\pi – \arccos b) + 2k\pi \,\,\,\, k \in \mathbb{Z}; $$

Esempio di risoluzione di un’equazione goniometrica elementare del tipo \( \sin x=a \)

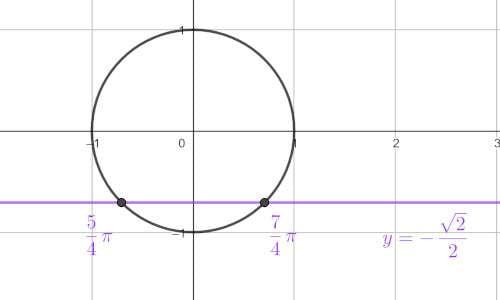
Si consideri l’equazione goniometrica \( \sin x = – \frac{\sqrt{2}}{2} \). Per risolverla l’obiettivo è trovare i punti della circonferenza goniometrica che abbiano l’ordinata pari a \( – \frac{\sqrt{2}}{2} \). Per fare ciò, si disegna la circonferenza goniometrica (ovvero una circonferenza centrata nell’origine degli assi con raggio pari a \( 1 \)) e successivamente si traccia una retta del tipo \( y=- \frac{\sqrt{2}}{2} \) e si trovano i punti di intersezione che rappresentano la soluzione cercata. La retta interseca la circonferenza in due punti, che corrispondono a due angoli: \( \frac{5}{4} \pi \) e \( \frac{7}{4} \pi \). Quindi l’equazione è soddisfatta per
$$ x= \frac{5}{4} \pi + 2k\pi \,\,\, \vee x= \frac{7}{4} \pi + 2k\pi . $$
Le soluzioni sono infinte al variare di \( k \in \mathbb{Z} \); il numero \( k \) è utilizzato per individuare tutte le possibili soluzioni tenendo conto della periodicità della funzione di \( 2\pi \).

Alternativamente per determinare le soluzioni di una equazione del tipo \( \sin x=a \) si può procedere nel seguente modo:

• Se \( a \) è un valore noto, ovvero corrisponde a un multiplo di 30°, 45°, 60°, indicando con \( \alpha\) l’angolo che soddisfa l’equazione \( \sin \alpha=a \), le soluzioni saranno del tipo: $$ x= \alpha + 2k\pi \,\,\, \vee x= (\pi – \alpha) + 2k\pi \,\,\,\, k \in \mathbb{Z}; $$
• Se \( a \) non è un valore noto, le soluzioni saranno del tipo:
  $$ x= \arcsin a + 2k\pi \,\,\, \vee x= (\pi – \arcsin a) + 2k\pi \,\,\,\, k \in \mathbb{Z}; $$

Equazioni goniometriche del tipo \( \tan x=c \) o \( \cot x=d \)

Per risolvere equazioni goniometriche elementari del tipo \( \tan x=c \) o \( \cot x=d \) è necessario ricordare come sono definite la tangente e la cotangente di un angolo. La tangente di un angolo è definita dal rapporto \( \frac{ \sin x }{\cos x} \) e, poiché il denominatore deve essere necessariamente diverso da \( 0 \), \( x \neq \frac{\pi}{2} + k\pi \,\,\,\, k \in \mathbb{Z} \). La cotangente di un angolo è definita dal rapporto \( \frac{ \cos x }{\sin x} \) e, poiché il denominatore deve essere necessariamente diverso da \( 0 \), \( x \neq k\pi \,\,\,\, k \in \mathbb{Z} \). Per risolvere un’equazione si deve disegnare la retta tangente o la retta cotangente, a seconda del tipo di equazione, e si devono individuare i punti, e quindi gli angoli, sulla circonferenza goniometrica che corrispondono all’intersezione della retta che collega il valore della tangente o della cotangente al centro della circonferenza goniometrica; i punti di intersezione tra la retta e la circonferenza goniometrica sono le soluzioni cercate.

Esempio di risoluzione di un’equazione goniometrica elementare del tipo \( \tan x=c \)

Si consideri l’equazione goniometrica \( \tan x = -\frac{\sqrt{3}}{3} \). Per risolverla l’obiettivo è trovare i punti della circonferenza goniometrica dati dall’intersezione della retta passante per il valore della tangente \( \frac{\sqrt{3}}{3} \) e l’origine. Per fare ciò, si disegna la circonferenza goniometrica (ovvero una circonferenza centrata nell’origine degli assi con raggio pari a \( 1 \)) e successivamente si traccia la retta tangente in \( x=1\), si traccia la retta tra il valore dato e l’origine e si identificano gli angoli corrispondenti ai punti di intersezione della retta con la circonferenza goniometrica. I due angoli cercati sono: \( \frac{\pi}{6} \) e \( \frac{7}{6} \pi \). Quindi l’equazione è soddisfatta per
$$ x= \frac{\pi}{6} + k\pi. $$

Le soluzioni sono infinte al variare di \( k \in \mathbb{Z} \); il numero \( k \) è utilizzato per individuare tutte le possibili soluzioni tenendo conto della periodicità della funzione di \( \pi \).

Alternativamente per determinare le soluzioni di una equazione del tipo \( \tan x=c \) si può procedere nel seguente modo:

• Se \( c \) è un valore noto, ovvero corrisponde a un multiplo di 30°, 45°, 60°, indicando con \( \gamma \) l’angolo che soddisfa l’equazione \( \tan \gamma = c \), le soluzioni saranno del tipo:
  $$ x= \gamma + k\pi \,\,\, k \in \mathbb{Z}; $$
• Se \( c \) non è un valore noto, le soluzioni saranno del tipo:
  $$ x= \arctan c + k\pi \,\,\, k \in \mathbb{Z}; $$

Esempio di risoluzione di un’equazione goniometrica elementare del tipo \( \cot x=d \)

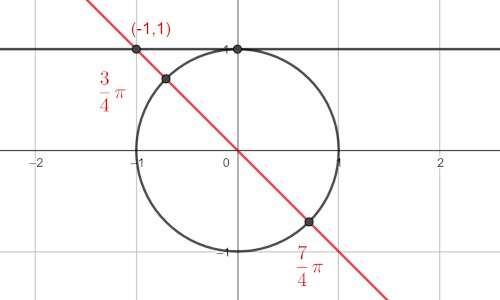
Si consideri l’equazione goniometrica \( \cot x = -1\). Per risolverla l’obiettivo è trovare i punti della circonferenza goniometrica dati dall’intersezione della retta passante per il valore della cotangente \( -1 \) e l’origine. Per fare ciò, si disegna la circonferenza goniometrica (ovvero una circonferenza centrata nell’origine degli assi con raggio pari a \( 1 \)) e successivamente si traccia la retta tangente in \( y=1\), si traccia la retta tra il valore dato e l’origine e si identificano gli angoli corrispondenti ai punti di intersezione della retta con la circonferenza goniometrica. I due angoli cercati sono: \( \frac{3 }{4} \pi \) e \( \frac{7}{4} \pi \). Quindi l’equazione è soddisfatta per
$$ x= \frac{3 }{4} \pi + k\pi. $$

Le soluzioni sono infinte al variare di \( k \in \mathbb{Z} \); il numero \( k \) è utilizzato per individuare tutte le possibili soluzioni tenendo conto della periodicità della funzione di \( \pi \).

Alternativamente per determinare le soluzioni di una equazione del tipo \( \tan x=d \) si può procedere nel seguente modo:

• Se \( d \) è un valore noto, ovvero corrisponde a un multiplo di 30°, 45°, 60°, indicando con \( \delta \) l’angolo che soddisfa l’equazione \( \cot \delta = d \), le soluzioni saranno del tipo:
  $$ x= \delta + k\pi \,\,\, k \in \mathbb{Z}; $$
• Se \( d \) non è un valore noto, le soluzioni saranno del tipo:
  $$ x= \mbox{arccot } d + k\pi \,\,\, k \in \mathbb{Z}; $$

Equazioni goniometriche del tipo \( \sec x=m \) o \( \csc x=n \)

Per quanto riguarda le funzioni secante e cosecante, si procede come per le funzioni seno e coseno, ricordando che \( \sec x = \frac{1}{\cos x} \), quindi \( x \neq \frac{\pi}{2} +k\pi \), e che \(\csc x=\frac{1}{\sin x} \), quindi \( x \neq \pi \).