Teorema di Bernoulli, dalla fisica alle applicazioni aerodinamiche

Il teorema di Bernoulli, o legge di Bernoulli è un ben noto teorema della fluidodinamica che è in grado di descrivere le condizioni di un fluido ideale all’interno di una tubazione, senza che su di esso venga compiuto alcun lavoro.

Per meglio comprendere tale teorema, lo si può considerare come il teorema sulla conservazione dell’energia meccanica applicato alla fluidodinamica, vale a dire che l’energia meccanica del sistema si conserva in assenza di forze non conservative, vale a dire se non viene compiuto alcun lavoro, l’energia meccanica del sistema si conserva.

Da un punto di vista euristico si può considerare il teorema sulla conservazione dell’energia meccanica che asserisce \(\frac{1}{2}mv^2 + mgh = costante\). Sfortunatamente per noi, la massa è una proprietà estensiva e quando si ha a che fare con i fluidi risulta difficile utilizzare proprietà estensive, di conseguenza si ricorre alle così dette proprietà intensive. Nel nostro caso, dividendo membro a membro per il volume di campione considerato, si potrà riscrivere il teorema in questo modo \(\frac{1}{2}\rho v^2 + \rho gh = costante\). In questo modo nella formula compare la densità, vale a dire una proprietà intensiva.

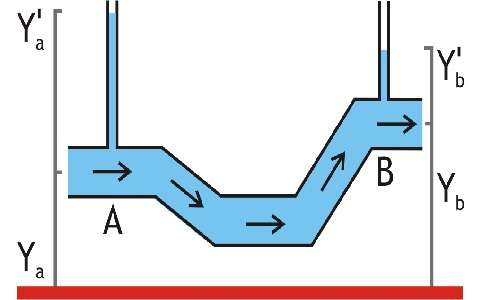
Tuttavia, per quanto possano essere semplici i metodi euristici non ci danno una dimostrazione soddisfacente del teorema. Consideriamo quindi un fluido ideale in una tubatura e prendiamo due sezioni della tubatura diverse \(dS_1\) e \(dS_2\). Per il teorema di Leonardo la massa che ha attraversato la sezione 1 nell’istante \(t\), sarà la stessa che attraverserà la sezione 2 nell’istante \(t + dt\). Pertanto la quantità di massa dm passante nelle due sezioni sarà pari a \(\rho dS_1 v_1 = \rho dS_2 v_2\). Andando ad applicare il teorema dell’energia meccanica, notiamo subito che l’unico lavoro che la forza peso può compiere, sarà dato dalla differenza di quota tra le due sezioni e quindi \(dL = dmg(z_1 – z_2)\). Vi è inoltre il lavoro delle forze di superficie, che è pari \(dL_s = dF_1 v_1 dt – dF_2 v_2 dt = \rho dS_1 v_1 dt – \rho dS_2 v_2 dt \) ed infine il lavoro dovuto alla variazione di energia cinetica all’interno della tubazione, vale a dire \(dK = \frac{1}{2}dmv_2^2 – \frac{1}{2}dmv_1^2\), di conseguenza il teorema assume la forma \(dmg(z_1 – z_2) = \frac{1}{2}dm(v_2^2 – v_1^2)\), e riarrangiando si ottiene \(dmg(z_1 – z_2) + \frac{(p_1 – p_2)dm}{\rho} = \frac{1}{2}dm(v_2^2 – v_1^2)\). Fatto ciò, separando i termini relativi alla sezione 1 dai termini relativi alla sezione 2 ed, eliminando la densità dal denominatore si ottiene \( p_1 + \rho gz_1 + \frac{1}{2}\rho v_1^2 = p_2 \rho gz_2 + \frac{1}{2}\rho v_2^2\) da cui si deduce che il termine \(p + \rho gz + \frac{1}{2}\rho v^2 = costante\) poiché le sezioni considerate nella dimostrazione sono scelte a caso lungo tutta la tubazione.

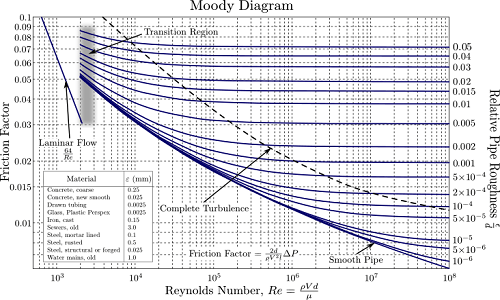
Se si considera invece l’applicazione del teorema di Bernoulli ad un fluido reale bisogna mettere in conto del lavoro delle forze di attrito che vengono a generarsi tra fluido e tubazione. Le perdite di carico vengono determinate attraverso l’equazione di Darcy-Weysbach \(y’ = \frac{\lambda L_{eq} v^2}{2dg}\), dove \(\lambda\) viene detto fattore di attrito, \(L_{eq}\) la lunghezza equivalente della tubazione (che tiene conto anche di eventuali curve e modificazioni del percorso, \(d\) è il diametro, mentre \(v\) e \(g\) sono la velocità del fluido e l’accelerazione di gravità. Il fattore di attrito dipende principalmente dalle condizioni di moto del liquido. Nel caso di un moto laminare, vale a dire per numero di Reynolds < 2000, il coefficiente di attrito viene calcolato attraverso la formula \(\lambda = \frac{64}{Re}\). Tuttavia, questa condizione non sempre si verifica nelle tubazioni o meglio, rappresenta una bassa percentuale dei casi reali. Nel caso di un moto turbolento, vale a dire con numero di Reynolds > 4000 il coefficiente di attrito dipende dalla scabrezza relativa del tubo ed il suo valore viene estrapolato dall’abaco di Moody.

Per sopperire alla dissipazione di energia e per tenere il fluido ad una velocità sufficiente, si introduce un termine al primo membro dell’equazione di Bernoulli che corrisponde all’energia che una pompa trasferisce al liquido. Tale termine prende il nome di prevalenza, H.

Tuttavia il teorema di Bernoulli, l’equazione di Darcy-Weysbach e la prevalenza per come sono enunciate sono incompatibili dal punto di vista delle unità di misura, avendo il primo l’unità di misura di una pressione e la seconda l’unità di misura di una lunghezza. Per far combaciare le due cose si può operare in due modi: dividere membro a membro il teorema di Bernoulli per il termine \(\rho g\), o viceversa moltiplicare prevalenza ed equazione di Darcy-Weisbach per lo stesso termine.

Una delle applicazioni più comuni del teorema di Bernoulli la troviamo nelle bombolette spray o nebulizzatori. La pressione all’interno del recipiente è più alta rispetto alla pressione atmosferica, infatti sostanze generalmente gassose o molto volatili (ad esempio i profumi) si trovano allo stato liquido e non evaporano per effetto dell’elevata pressione del recipiente. Ad ogni modo, nel momento in cui la valvola del recipiente viene aperta, si crea una differenza di pressione che deve essere compensata da una fuoriuscita di fluido. Maggiore è la differenza di pressione, maggiore sarà la velocità di efflusso.

Un’altra applicazione del teorema di Bernoulli è la cosiddetta portanza, vale a dire l’effetto che sfruttano gli aeroplani o le auto da corsa per affrontare le varie fasi di volo o per essere più stabili.

La portanza è una forza, che si viene a generare a causa della differenza di pressione totale che si viene a formare sulle due superfici di un’ala/alettone. A seconda di come è orientata l’ala, l’aria scorrerà con velocità diversa lungo le due superfici. Dall’equazione di Bernoulli, sappiamo che ad una velocità più bassa corrisponde una pressione più alta, mentre ad una velocità più alta corrisponde una pressione più bassa. A questo punto, se l’ala ha una curvatura rivolta verso l’alto, il flusso d’aria è come se andasse incontro ad una strozzatura, favorendo quindi una velocità più alta sulla parte superiore dell’ala. Ciò garantisce una pressione totale più alta nella parte inferiore e di conseguenza una spinta dal basso verso l’alto.

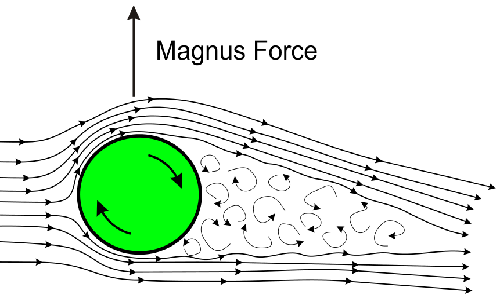
Un ultimo effetto del Teorema di Bernoulli è l’effetto Magnus, che viene applicato tantissime volte nello sport, come ad esempio il tennis o il calcio. Immaginiamo di avere a che fare con una palla lanciato in avanti, e che la palla ruoti in senso antiorario. A causa dell’attrito viscoso, la palla trascina con se l’aria che la circonda, mentre l’aria presente sulla traiettoria della palla scorre nel verso opposto al moto della palla. Ruotando in senso antiorario, sul lato destro la palla porta in avanti alcune molecole d’aria che vanno a scontrarsi con le molecole che scorrono in verso opposto, di conseguenza, in ossequio alla legge di Bernoulli, l’aria sul lato destro scorrerà più lentamente rispetto al lato sinistro, dove l’aria trascinata dalla palla avrà verso concorde rispetto al flusso presente sulla traiettoria e di conseguenza a velocità più alta. Come per la portanza, a velocità superiore corrisponde pressione totale inferiore, di conseguenza se lasciata ruotare in senso antiorario la palla riceverà una spinta da destra verso sinistra.