I logaritmi: definizione e applicazioni

COSA SONO I LOGARITMI?

I logaritmi sono degli operatori matematici indicati generalmente con \( \log_a b \). Il logaritmo di un numero in una determinata base (\( a \)) è l’esponente a cui si deve elevare la base per ottenere il numero stesso. I logaritmi vennero introdotti all’inizio del XVII secolo da Nepero; trovano un’ampia applicazione nelle scienze e nell’ingegneria, soprattutto per la semplificazione dei calcoli molto grandi mediante l’utilizzo delle tavole logaritmiche. I logaritmi trovano applicazione anche nella vita quotidiana, infatti i nostri sensi sono in scala logaritmica: se ascoltiamo un suono e poi un altro suono che sembra di intensità doppia, se lo si misura, si nota che ha un’intensità quattro volte superiore; stessa cosa avviene con i fenomeni luminosi.

Definizione di logaritmo

Dati due numeri \( a, b \) reali positivi, con \( a \neq 1 \), si definisce logaritmo in base \( a \) di \( b \) l’esponente a cui elevare \( a \) per ottenere \( b \), ovvero
$$ c=\log_a b$$
è il numero tale che \( a^c=b \). Le condizioni su \( a \) e \( b \) sono necessarie per l’esistenza e unicità di \( c \), infatti:

• se \( a =0 \) e \( b=0 \) esistono infiniti valori di \( c \) che soddisfano la relazione;
• se \( a =0 \) e \( b\neq 0 \) non esistono \( c \) tali che \( a^c=b \);
• se \( a =1 \) e \( b\neq 1\) non esistono \( c \) con tale proprietà, infatti non esistono numeri diversi da \( 1 \) che possano essere ottenuti come potenza di \( 1 \);
• \( a =1 \) e \( b = 1\) esistono infiniti valori di \( c \) che soddisfano la relazione;
• se \( a<0 \) la relazione non è definita per ogni \( c \) reale. Può essere definito per ogni \( a \) reale solo coi numeri razioni esprimibili mediante una frazione con denominatore dispari e di conseguenza anche i numeri interi.

Poiché il risultato di un elevamento a potenza è positivo, \( b \) deve essere necessariamente positivo.

Proprietà dei logaritmi

I logaritmi presentano molte proprietà interessanti che permettono notevolmente di semplificare il calcolo dei logaritmi:

• \( \log_a 1=0 \)
• \( \log_a a=0 \)
• \( a^{\log_a(b)}= \log_a(a^b)=b\)
• Logaritmo del prodotto: \( \log_a (b \cdot c)=\log_a b + \log_a c \)
• Logaritmo di una potenza: \( \log_a b^k=k \log_a b \)
• Logaritmo del quoziente: \( \log_a (\frac{b}{c})=\log_a b – \log_a c \)
• Cambiamento di base: \( log_a b= \frac{\log_c b}{\log_c a} \)

Logaritmo del prodotto

Il logaritmo del prodotto di due numeri positivi è uguale alla somma dei logaritmi dei singoli numeri:
$$ \log_a (b \cdot c)=\log_a b + \log_a c. $$
Si pongono \( x= \log_a b \) e \( y= \log_a c \). Per la definizione dei logaritmi \( a^x=b \) e \( a^y=c \). Moltiplicando membro a membro si ottiene:
$$ a^x \cdot a^y =b \cdot c,$$
Usando le proprietà delle potenze si può scrivere:
$$ a^{x+y} = b \cdot c. $$
Per la definizione di logaritmo
$$ x + y= \log_a (b\cdot c), $$
Sostituendo le espressioni iniziali e utilizzando la proprietà simmetrica dell’uguaglianza si ottiene la tesi:
$$ \log_a (b \cdot c)=\log_a b + \log_a c. $$

Logaritmo di una potenza

Il logaritmo della potenza di un numero positivo elevato ad un esponente reale è uguale al prodotto dell’esponente per il logaritmo del numero:
$$ \log_a b^k=k \log_a b. $$
Posto \( x= \log_a b \), per la definizione dei logaritmi \( a^x=b \). Elevando a \( k \) tutti e due i membri si ottiene:
$$ (a^x)^k=b^k, $$
Usando la proprietà delle potenze, si può scrivere:
$$a^{kx}=b^k. $$
Per la definizione di logaritmo
$$ k \cdot x= \log_a b^k $$
Sostituendo le espressioni iniziali e utilizzando la proprietà simmetrica dell’uguaglianza si ottiene la tesi:
$$ \log_a b^k=k \log_a b. $$
Da questa proprietà deriva che:
$$ \log_a \sqrt[k]{x}=\frac{1}{k} \log_a x, $$
$$ \log_a \frac{1}{x}= – \log_a x. $$

Logaritmo del quoziente

Il logaritmo del quoziente di due numeri positivi è uguale alla differenza del logaritmo del numeratore e del logaritmo del denominatore:
$$ \log_a (\frac{b}{c})=\log_a b  –  \log_a c $$
Si pongono \( x= \log_a b \) e \( y= \log_a c \). Per la definizione dei logaritmi \( a^x=b \) e \( a^y=c \). Dividendo membro a membro si ottiene:
$$\frac{ a^x}{ a^y} =\frac{b}{c},$$
Usando le proprietà delle potenze si può scrivere:
$$ a^{x-y} =\frac{b}{c}.$$
Per la definizione di logaritmo
$$ x – y= \log_a (\frac{b}{c}), $$
Sostituendo le espressioni iniziali e utilizzando la proprietà simmetrica dell’uguaglianza si ottiene la tesi:
$$ \log_a (b \cdot c)=\log_a b   – \log_a c. $$

Cambiamento di base

Per cambiare la base di un logaritmo si può, a partire da \( a, b, c >0 \), usare la seguente formula:
$$ log_a b= \frac{\log_c b}{\log_c a}. $$
Posto \( x= \log_a b \), per la definizione dei logaritmi \( a^x=b \), quindi le due espressioni sono equivalenti. A questo punto si può calcolare il logaritmo in base \( c \) di entrambi i membri della seconda uguaglianza:
$$ \log_c a^x = \log_c b. $$
Per la proprietà del logaritmo di una potenza, si può scrivere:
$$ x \log_c a = \log_c b, $$
poi, dividendo per \( \log_c a \) entrambi i membri (sicuramente \( \log_c a \neq 0 \) poiché \( a \neq 1 \)) si ottiene:
$$ x= \frac{\log_c b}{\log_c a}. $$
Sostituendo l’espressione iniziale si ottiene la tesi:
$$ log_a b= \frac{\log_c b}{\log_c a}. $$

STORIA DEI LOGARITMI

I logaritmi vennero introdotti per la prima volta nel 1614 da Nepero nel suo libro Mirifici Logarithmorum Canonis Descriptio, con la speranza di fornire uno strumento che rendesse più veloci i calcoli degli astronomi. L’idea di Nepero fu quella di utilizzare una progressione geometrica per poter effettuare il prodotto tra due numeri solamente mediante l’utilizzo delle potenze. Tuttavia, i termini della progressione, utilizzando le potenze con base \( 10 \), sono molto distanti tra loro, quindi Nepero, per introdurre i logaritmi Nepero costruì una serie geometrica di ragione vicina ad \( 1 \) in modo da evitare il problema; scelse come base \( 1- \frac{1}{10^7} \) (circa \( 0,9999999 \) e moltiplicò le potenze successive della base base per \( 10^7 \) per ottenere maggiore equilibrio ed evitare troppe cifre decimali. Se \( N=10^7 \bigl(1- \frac{1}{10^7}\bigr)^L=10^7, \) allora \( \bigl(1- \frac{1}{10^7}\bigr)^L =1 \), quindi necessariamente \( L=0\). Se si indica con \(Neplog x \) il logaritmo di Nepero, allora:
$$ Neplog (10^7) =0,$$
$$ Neplog (9999999)=1. $$
Infatti in questo caso si avrà \( 10^7 \bigl(1- \frac{1}{10^7}\bigr)^L=10^7 \bigl(1- \frac{1}{10^7}\bigr) \), quindi necessariamente \( L=1 \). Inoltre il logaritmo di Nepero soddisfa la seguente espressione
$$ Neplog (10^7 a\cdot b)= Neplog (a) + Neplog (b). $$
Inoltre \( \bigl(1- \frac{1}{10^7}\bigr)^{10^7} \approx \frac{1}{e}. \) L’invenzione di Nepero fu molto acclamata. Il logaritmo naturale venne descritto per la prima volta nel 1668 da Nicolaus Mercator nel suo scritto Logarithmotechnia. Intorno agli anni trenta del Settecento, Eulero invece definì le funzioni esponenziale e logaritmica come:
$$ e^x = \lim_{n \rightarrow +\infty} \bigl(1+\frac{x}{n}\bigr)^n, $$
$$\ln (x)= \lim_{n \rightarrow +\infty} n(x^{\frac{1}{n}} -1).$$
Egli dimostrò anche che queste funzioni sono l’una l’inversa dell’altra.

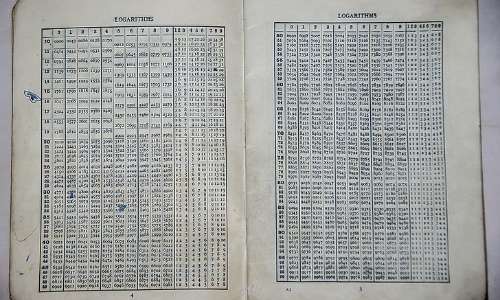
Tavole dei logaritmi

I logaritmi trovarono un ampio utilizzo soprattutto in astronomia, grazie all’utilizzo delle tavole logaritmiche. La prima tavola venne completata nel 1617 da Henry Briggs e successivamente vennero scritte tavole sempre più precise. Su queste tavole veniva elencato il valore di \(\log_b x \) e di \( b^x \) per ogni numero \( x \) di un certo intervallo, con una base \( b \) scelta e con una precisione fissata. Per esempio, la tavola di Briggs conteneva il logaritmo in base \(10\) dei numeri da \( 1 \) a \( 1000 \) con una precisione di otto cifre decimali. Grazie all’uso di queste tavole era possibile calcolare facilmente il prodotto e il quoziente di due numeri:
$$ c \cdot d = b^{\log_b c} \cdot b^{\log_b d}= b^{\log_b c + \log_b d};$$
$$ \frac{c}{d} = c \cdot d^{-1} = b^{\log_b c – \log_b d}.$$
Anche il calcolo delle potenze e delle radici veniva ulteriormente semplificato:
$$ c^d= (b^{\log_b c})^d= b^{d\cdot \log_b c}; $$
$$\sqrt[d] c = c^{\frac{1}{d}}= b^{\frac{1}{d} \cdot \log_b c}. $$
La funzione \( b^x \) venne chiamata antilogaritmo, poiché inversa del logaritmo.

FUNZIONE LOGARITMICA

La funzione logaritmica \( f: (0,+\infty) \rightarrow \mathbb{R} \) è del tipo
$$ y=\log_a x, $$
con \( a>0, a\neq 1 \). La funzione logaritmica è la funzione inversa della funzione esponenziale: i grafici delle due funzioni sono simmetrici rispetto alla bisettrice del primo e terzo quadrante (la retta di equazione \( y=x \)). La funzione logaritmica presenta alcune proprietà:

• Ha dominio \( \mathbb{R^+} \) e codominio \( \mathbb{R} \);
• È una funzione biunivoca, sempre crescente se \( a>1 \) e sempre decrescente se \( 0<a<1 \);
• Il grafico interseca l’asse \( x \) nel punto \( (0,1) \).

La funzione logaritmo è derivabile e la sua derivata è
$$ \frac{d}{dx} \log_a x = \frac{1}{x \ln a }. $$
Essendo una funzione continua, è integrabile e il suo integrale, applicando l’integrazione per parti è il seguente:
$$ \int \log_a x dx= x \log_a x – \frac{x}{\ln a} + c= x \log_a {\frac{x}{e}} +c. $$